Was heisst «Mathematik betreiben»? Oft wird darunter das Lernen und Anwenden von Rechentechniken verstanden. Rechentechniken sind aber nur der Werkzeugkasten, mit dessen Hilfe mathematische Situationen untersuchen werden können. Spannende Mathematik betreiben heisst, einen Sachverhalt zu analysieren und zu durchschauen, Erklärungen zu mathematischen Phänomenen zu finden.
Unten finden sich mathematische Situationen für die Jahrgangsstufen 9 – 10, welche Lernende eigenständig untersuchen können. Zu jeder Situation finden sich einige Basisinformationen: Der mathematische Themenbereich und etwas präziser das mathematische Thema, die (ungefähre) Jahrgangsstufe und eine Einschätzung des Schwierigkeitsgrades (1 = für alle zugänglich, 5 = für gymnasiale Stufe).
Der erste Link führt zur mathematischen Situation und den Fragestellungen, welche von den Lernenden zu untersuchen sind. Für die Dokumentation der Erkenntnisse ist das Arbeitsblatt gedacht, welches die Lehrperson herunterladen, allenfalls anpassen und kopieren kann. Zu Beginn des Arbeitsblattes finden sich noch einmal die Fragestellungen, für die Antworten der Lernenden hat sich die offene Form mit Textzeilen und Feldern für Skizzen bewährt. Im Dokument «Hinweise für die Lehrperson» finden sich eine Beschreibung des mathematischen Sachverhaltes, eine Liste hilfreicher mathematischer Begriffe, Hinweise zu den Lösungen, weiterführende Fragestellungen sowie eine Einordnung in den Deutschschweizer Lehrplan 21.
Eine Übersicht über alle mathematischen Situationen zum Download findet sich hier.
Der Flächengraph (Sachrechnen, Funktionen)
Jahrgangsstufe: 9 Schwierigkeitsgrad: 3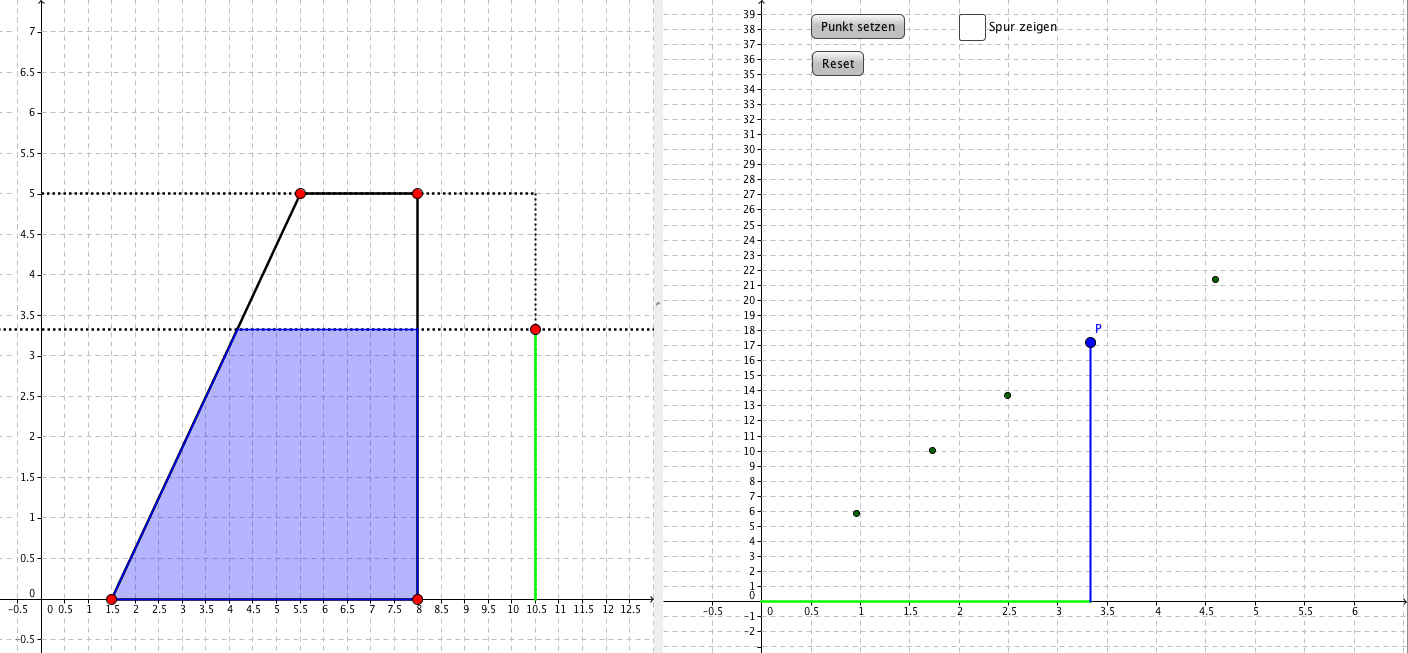
Wie verläuft der Graph, welcher die Zunahme des Flächeninhalts eines Vierecks angibt?
Link zur mathematischen Situation: «Der Flächengraph»
Arbeitsblatt zur Dokumentation: «Der Flächengraph- Arbeitsblatt»
Hinweise für Lehrpersonen: «Der Flächengraph- Hinweise für Lehrpersonen»
Die lineare Funktion (Sachrechnen, Lineare Funktion)
Jahrgangsstufe: 9 Schwierigkeitsgrad: 2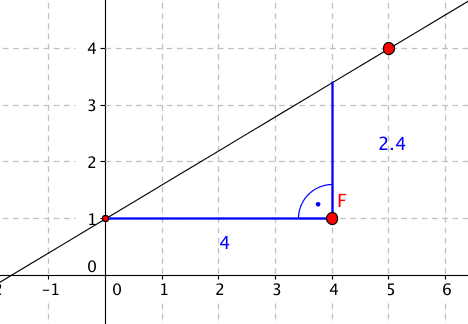
Was lässt sich über Steigungsdreiecke von linearen Funktionen sagen?
Link zur mathematischen Situation: «Die lineare Funktion»
Arbeitsblatt zur Dokumentation: «Die lineare Funktion – Arbeitsblatt»
Hinweise für Lehrpersonen: «Die lineare Funktion – Hinweise für Lehrpersonen»
Die erste binomische Formel (Arithmetik und Algebra, algebraische Terme)
Jahrgangsstufe: 9 Schwierigkeitsgrad: 2
Wie können Terme der Form (a + b) · (a + b) berechnet werden?
Link zur mathematischen Situation: «Die erste binomische Formel»
Arbeitsblatt zur Dokumentation: «Die erste binomische Formel – Arbeitsblatt»
Hinweise für Lehrpersonen: «Die erste binomische Formel – Hinweise für Lehrpersonen»
Summen natürlicher Zahlen (Arithmetik und Algebra, Terme)
Jahrgangsstufe: 9 Schwierigkeitsgrad: 4
Wie lassen sich Summen wie 1 + 2 + 3 + … 99 + 100 berechnen?
Link zur mathematischen Situation: «Summen natürlicher Zahlen»
Arbeitsblatt zur Dokumentation: «Summen natürlicher Zahlen – Arbeitsblatt»
Hinweise für Lehrpersonen: «Summen natürlicher Zahlen – Hinweise für Lehrpersonen»
Diagonalen in regelmässigen Vielecken (Geometrie, Vielecke; Algebra, Summenformel; Kombinatorik)
Jahrgangsstufe: 9 Schwierigkeitsgrad: 4
Wie viele Diagonalen hat ein n-Eck?
Link zur mathematischen Situation: «Diaogonalen in regelmässigen Vielecken»
Arbeitsblatt zur Dokumentation: «Diaogonalen in regelmässigen Vielecken – Arbeitsblatt»
Hinweise für Lehrpersonen: «Diaogonalen in regelmässigen Vielecken – Hinweise für Lehrpersonen»
Das Kleine Sterndodekaeder (Geometrie, regelmässige Körper)
Jahrgangsstufe: 9-10 Schwierigkeitsgrad: 3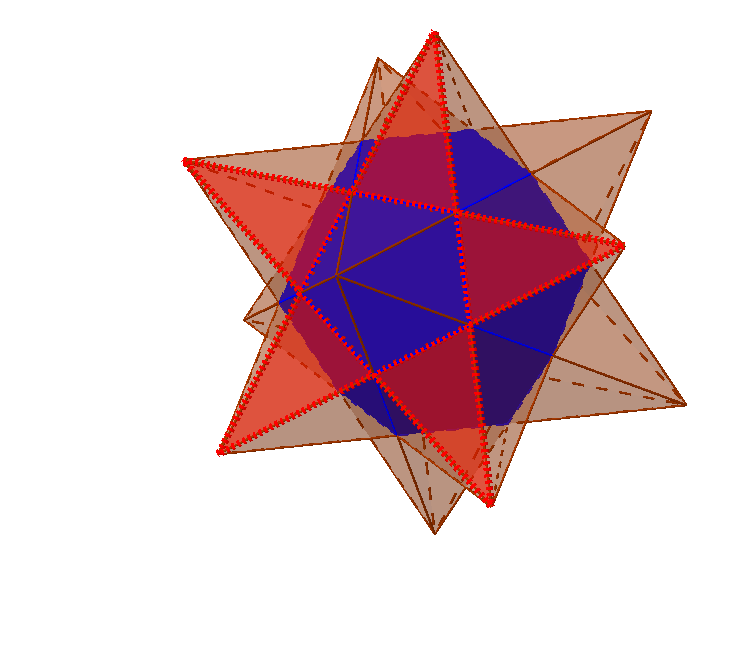
Untersuche das kleine Sterndodekaeder.
Das kleine Sterndodekaeder ist einer der vier Kepler-Poinsot-Körper. Dieser Körper ist regelmässig wie die bekannten platonischen Körper (regelmässiges Tetraeder, Hexaeder, Oktaeder, Dodekaeder und Ikosaeder), aber nicht konvex, er hat «Spitzen». Benannt sind die Kepler-Poinsot-Körper zu Ehren von Johannes Kepler (1571-1630) und Louis Poinsot (1777-1859).
Link zur mathematischen Situation in Farbe: «Das Kleine Sterndodekaeder»
Link zur mathematischen Situation mit einer Blau-Rot-3D-Brille: «Das Kleine Sterndodekaeder – 3D»
Arbeitsblatt zur Dokumentation: «Das Kleine Sterndodekaeder – Arbeitsblatt»
Hinweise für Lehrpersonen: «Das Kleine Sterndodekaeder – Hinweise für Lehrpersonen»
Das Grosse Sterndodekaeder (Geometrie, regelmässige Körper)
Jahrgangsstufe: 9-10 Schwierigkeitsgrad: 3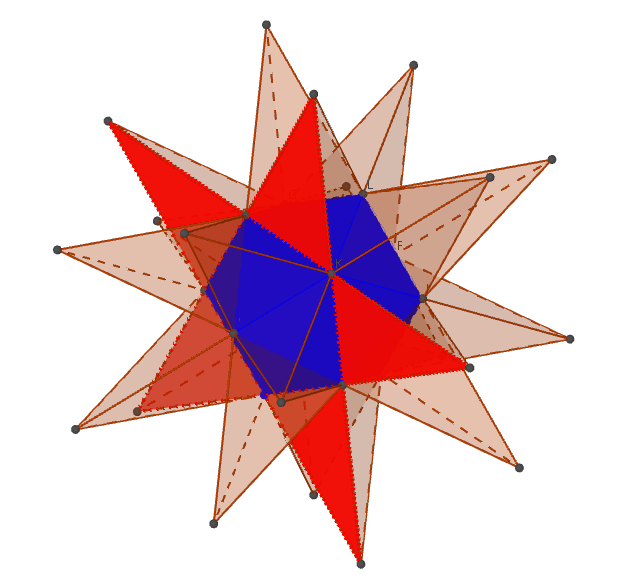
Untersuche das grosse Sterndodekaeder.
Das grosse Sterndodekaeder ist einer der vier Kepler-Poinsot-Körper. Dieser Körper ist regelmässig wie die bekannten platonischen Körper (regelmässiges Tetraeder, Hexaeder, Oktaeder, Dodekaeder und Ikosaeder), aber nicht konvex, er hat «Spitzen».
Link zur mathematischen Situation in Farbe: «Das Grosse Sterndodekaeder»
Link zur mathematischen Situation mit einer Blau-Rot-3D-Brille: «Das Grosse Sterndodekaeder – 3D»
Arbeitsblatt zur Dokumentation: «Das Grosse Sterndodekaeder – Arbeitsblatt»
Hinweise für Lehrpersonen: «Das Grosse Sterndodekaeder – Hinweise für Lehrpersonen»
Das Grosse Dodekaeder (Geometrie, regelmässige Körper)
Jahrgangsstufe: 9-10 Schwierigkeitsgrad: 3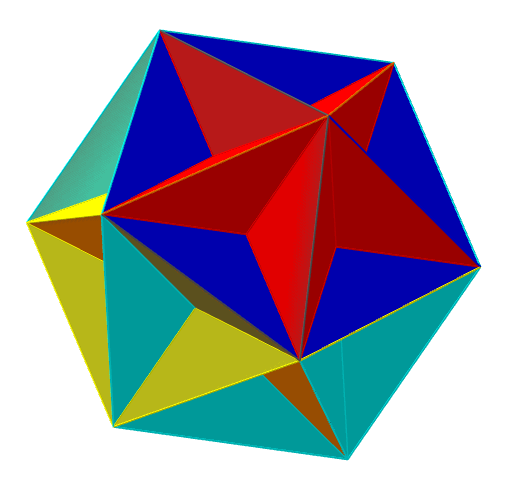
Untersuche das grosse Dodekaeder.
Das grosse Dodekaeder ist einer der vier Kepler-Poinsot-Körper. Dieser Körper ist regelmässig wie die bekannten platonischen Körper (regelmässiges Tetraeder, Hexaeder, Oktaeder, Dodekaeder und Ikosaeder, aber nicht konvex, er hat «Spitzen». In Puzzler-Kreisen wird er auch «Alexander’s Star» genannt und er ist auch als Puzzle der Rubik’s Cube-Familie erhältlich.
Link zur mathematischen Situation in Farbe: «Das Grosse Dodekaeder»
Link zur mathematischen Situation mit einer Blau-Rot-3D-Brille: «Das Grosse Dodekaeder – 3D»
Link zur mathematischen Situation mit hervorgehobenen Sternen in Farbe: «Das Grosse Dodekaeder (Sterne hervorgehoben)»
Link zur mathematischen Situation mit hervorgehobenen Sternen mit einer Blau-Rot-3D-Brille: «Das Grosse Dodekaeder (Sterne hervorgehoben) – 3D»
Arbeitsblatt zur Dokumentation: «Das Grosse Dodekaeder – Arbeitsblatt»
Hinweise für Lehrpersonen: «Das Grosse Dodekaeder – Hinweise für Lehrpersonen»