Was heisst «Mathematik betreiben»? Oft wird darunter das Lernen und Anwenden von Rechentechniken verstanden. Rechentechniken sind aber nur der Werkzeugkasten, mit dessen Hilfe mathematische Situationen untersuchen werden können. Spannende Mathematik betreiben heisst, einen Sachverhalt zu analysieren und zu durchschauen, Erklärungen zu mathematischen Phänomenen zu finden.
Unten finden sich mathematische Situationen der Jahrgangsstufen 7 und 8, welche Lernende eigenständig untersuchen können. Zu jeder Situation finden sich einige Basisinformationen: Der mathematische Themenbereich und etwas präziser das mathematische Thema, die (ungefähre) Jahrgangsstufe und eine Einschätzung des Schwierigkeitsgrades (1 = für alle zugänglich, 5 = für gymnasiale Stufe).
Der erste Link führt zur mathematischen Situation und den Fragestellungen, welche von den Lernenden zu untersuchen sind. Für die Dokumentation der Erkenntnisse ist das Arbeitsblatt gedacht, welches die Lehrperson herunterladen, allenfalls anpassen und kopieren kann. Zu Beginn des Arbeitsblattes finden sich noch einmal die Fragestellungen, für die Antworten der Lernenden hat sich die offene Form mit Textzeilen und Feldern für Skizzen bewährt. Im Dokument «Hinweise für die Lehrperson» finden sich eine Beschreibung des mathematischen Sachverhaltes, eine Liste hilfreicher mathematischer Begriffe, Hinweise zu den Lösungen, weiterführende Fragestellungen sowie eine Einordnung in den Deutschschweizer Lehrplan 21.
Das drehende Quadrat (Geometrie, Flächeninhalte ebener Figuren)
Jahrgangsstufe: 7 Schwierigkeitsgrad: 1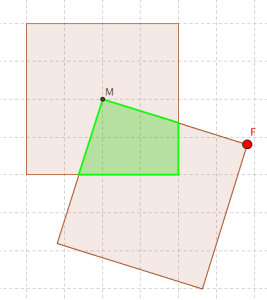
Ein Quadrat dreht sich um ein anderes Quadrat. Wie gross ist der gemeinsame Flächenanteil?
Link zur mathematischen Situation: «Das drehende Quadrat»
Arbeitsblatt zur Dokumentation: «Das drehende Quadrat – Arbeitsblatt»
Hinweise für Lehrpersonen: «Das drehende Quadrat – Hinweise für Lehrpersonen»
Der Billardstoss (Geometrie, Achsenspiegelung)
Jahrgangsstufe: 7 Schwierigkeitsgrad: 1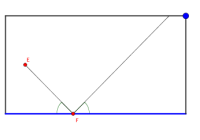
In welche Richtung ist ein Billardball anzustossen, dass er via eine Bande
in eine Ecke des Tisches gespielt wird?
Link zur mathematischen Situation: «Der Billardstoss»
Arbeitsblatt zur Dokumentation: «Der Billardstoss – Arbeitsblatt»
Hinweise für Lehrpersonen: «Der Billardstoss – Hinweise für Lehrpersonen»
Das Spiegelbild (Geometrie, Abbildungen)
Jahrgangsstufe: 7 Schwierigkeitsgrad: 2
Wie gross muss ein Spiegel sein, damit man sich darin ganz sieht?
Link zur mathematischen Situation: «Das Spiegelbild»
Arbeitsblatt zur Dokumentation: «Das Spiegelbild – Arbeitsblatt»
Hinweise für Lehrpersonen: «Das Spiegelbild – Hinweise für Lehrpersonen»
Gespiegelte Dreiecke (Geometrie, Kongruenzabbildungen)
Jahrgangsstufe: 7 Schwierigkeitsgrad: 1
Welche interessanten Situationen entstehen bei der Spiegelung eines Dreiecks?
Link zur mathematischen Situation: «Gespiegelte Dreiecke»
Arbeitsblatt zur Dokumentation: «Gespiegelte Dreiecke – Arbeitsblatt»
Hinweise für Lehrpersonen: «Gespiegelte Dreiecke – Hinweise für Lehrpersonen»
Achsen- und Punktspiegelung (Geometrie, Kongruenzabbildungen)
Jahrgangsstufe: 7 Schwierigkeitsgrad: 4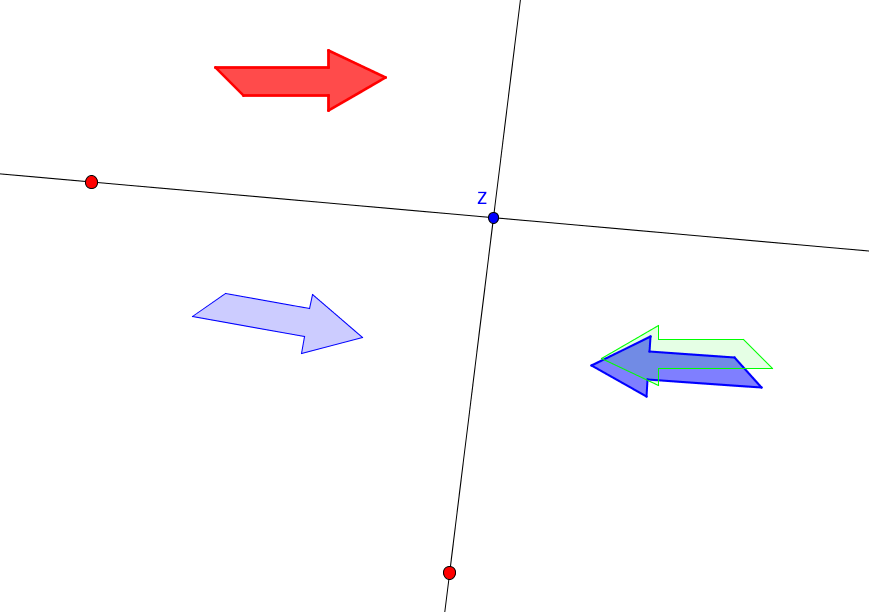
Wie kann eine Punktspiegelung durch zwei Achsenspiegelungen ersetzt werden?
Link zur mathematischen Situation: «Achsen- und Punktspiegelung»
Arbeitsblatt zur Dokumentation: «Achsen- und Punktspiegelung – Arbeitsblatt»
Hinweise für Lehrpersonen: «Achsen- und Punktspiegelung – Hinweise für Lehrpersonen»
Die Schatzsuche (Geometrie, Kongruenzabbildungen)
Jahrgangsstufe: 7 Schwierigkeitsgrad: 5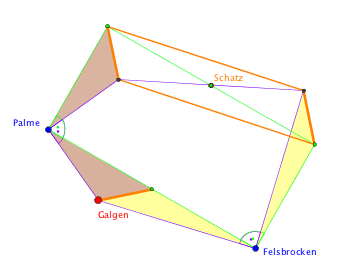
Wie kann der Schatz gefunden werden, wenn nicht alle Informationen vorhanden sind?
Link zur mathematischen Situation: «Die Schatzsuche»
Arbeitsblatt zur Dokumentation: «Die Schatzsuche – Arbeitsblatt»
Hinweise für Lehrpersonen: «Die Schatzsuche – Hinweise für Lehrpersonen»
Dreiecktypen (Geometrie, Dreiecke)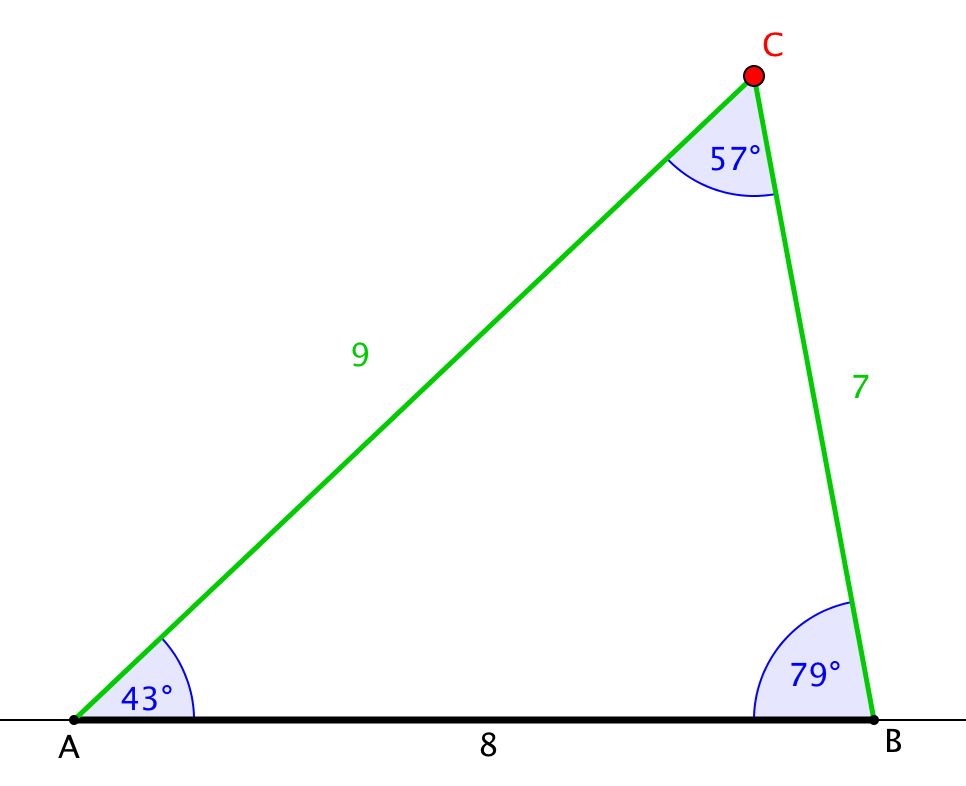
Jahrgangsstufe: 7 Schwierigkeitsgrad: 1
Welche Dreiecksformen ergeben sich über einer fixen Seite AB?
Link zur mathematischen Situation (ohne Hilfslinien): «Dreiecktypen»
Link zur mathematischen Situation (mit Hilfslinien): «Dreiecktypen»
Arbeitsblatt zur Dokumentation: «Dreiecktypen – Arbeitsblatt»
Hinweise für Lehrpersonen: «Dreiecktypen – Hinweise für Lehrpersonen»
Innen- und Aussenwinkel am Dreieck (Geometrie, Dreiecke)
Jahrgangsstufe: 7 Schwierigkeitsgrad: 1
Welche Zusammenhänge bestehen zwischen Innen- und Aussenwinkeln am Dreieck?
Link zur mathematischen Situation: «Innen- und Aussenwinkel am Dreieck»
Arbeitsblatt zur Dokumentation: «Innen- und Aussenwinkel am Dreieck – Arbeitsblatt»
Hinweise für Lehrpersonen: «Innen- und Aussenwinkel am Dreieck – Hinweise für Lehrpersonen»
Drei Strecken im gleichseitigen Dreieck (Geometrie, Dreiecke)
Jahrgangsstufe: 7 Schwierigkeitsgrad: 3
Welche Eigenschaft besitzen drei Strecken in einem gleichseitigen Dreieck?
Link zur mathematischen Situation: «Drei Strecken im gleichseitigen Dreieck»
Arbeitsblatt zur Dokumentation: «Drei Strecken im gleichseitigen Dreieck – Arbeitsblatt»
Hinweise für Lehrpersonen: «Drei Strecken im gleichseitigen Dreieck – Hinweise für Lehrpersonen»
Sechs Dreiecke im gleichseitigen Dreieck (Geometrie, Dreiecke)
Jahrgangsstufe: 7 Schwierigkeitsgrad: 3
Welche Eigenschaft besitzen sechs Dreiecke in einem gleichseitigen Dreieck?
Link zur mathematischen Situation: «Sechs Dreiecke im gleichseitigen Dreieck»
Arbeitsblatt zur Dokumentation: «Sechs Dreiecke im gleichseitigen Dreieck – Arbeitsblatt»
Hinweise für Lehrpersonen: «Sechs Dreiecke im gleichseitigen Dreieck – Hinweise für Lehrpersonen»
Schwerliniendreiecke (Geometrie, Dreiecke)
Jahrgangsstufe: 7 Schwierigkeitsgrad: 3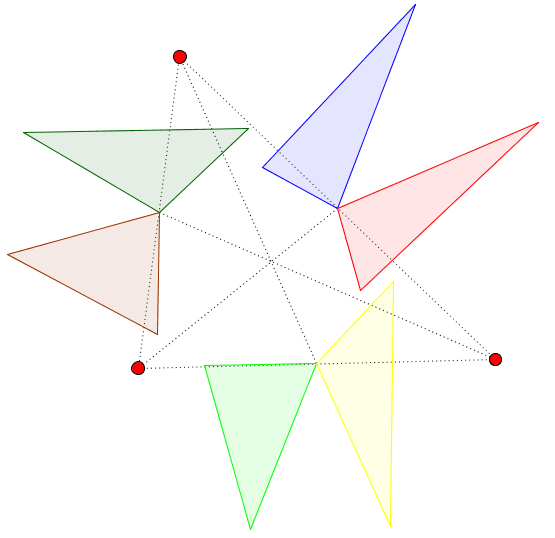
Welche überraschende Eigenschaft besitzen sechs Teildreiecke in einem Dreieck?
Link zur mathematischen Situation: «Schwerliniendreiecke»
Arbeitsblatt zur Dokumentation: «Schwerliniendreiecke – Arbeitsblatt»
Hinweise für Lehrpersonen: «Schwerliniendreiecke – Hinweise für Lehrpersonen»
Vierecksparkette (Geometrie, Vierecke)
Jahrgangsstufe: 7 Schwierigkeitsgrad: 2
Kann mit allen Vierecksformen ein Parkett gelegt werden?
Link zur mathematischen Situation: «Vierecksparkette»
Arbeitsblatt zur Dokumentation: «Vierecksparkette – Arbeitsblatt»
Hinweise für Lehrpersonen: «Vierecksparkette – Hinweise für Lehrpersonen»
Vierecke und Winkelhalbierende (Geometrie, Vierecke)
Jahrgangsstufe: 7 Schwierigkeitsgrad: 3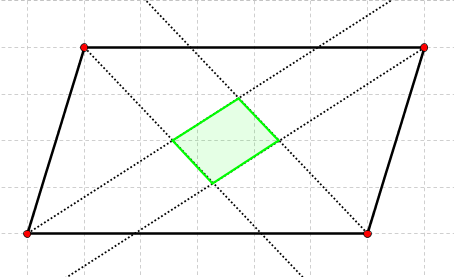
Welche Figuren entsteht, wenn in einem Viereck die Winkelhalbierenden eingezeichnet werden?
Link zur mathematischen Situation: «Vierecke und Winkelhalbierende»
Arbeitsblatt zur Dokumentation: «Vierecke und Winkelhalbierende – Arbeitsblatt»
Hinweise für Lehrpersonen: «Vierecke und Winkelhalbierende – Hinweise für Lehrpersonen»
Vierecke und Mittelsenkrechten (Geometrie, Vierecke)
Jahrgangsstufe: 7 Schwierigkeitsgrad: 3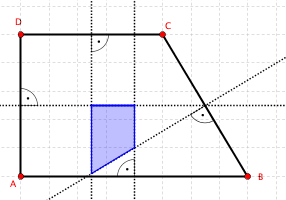
Welche Figuren entsteht, wenn in einem Viereck die Mittelsenkrechten eingezeichnet werden?
Link zur mathematischen Situation: «Vierecke und Mittelsenkrechten»
Arbeitsblatt zur Dokumentation: «Vierecke und Mittelsenkrechten – Arbeitsblatt»
Hinweise für Lehrpersonen: «Vierecke und Mittelsenkrechten – Hinweise für Lehrpersonen»
Das Mittenviereck (Geometrie, Vierecke)
Jahrgangsstufe: 7 Schwierigkeitsgrad: 3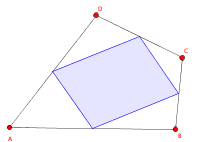
Welche Form hat das entstehende Viereck, wenn man die Seitenmitten eines Vierecks verbindet?
Link zur mathematischen Situation: «Das Mittenviereck»
Arbeitsblatt zur Dokumentation: «Das Mittenviereck – Arbeitsblatt»
Hinweise für Lehrpersonen: «Das Mittenviereck – Hinweise für Lehrpersonen»
Zwei Rechtecke im Rechteck (Geometrie, Vierecke)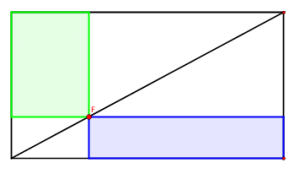
Jahrgangsstufe: 7 Schwierigkeitsgrad: 4
Welche Eigenschaft besitzen zwei Rechtecke in einem grösseren Rechteck?
Link zur mathematischen Situation: «Zwei Rechtecke im Rechteck»
Arbeitsblatt zur Dokumentation: «Zwei Rechtecke im Rechteck – Arbeitsblatt»
Hinweise für Lehrpersonen: «Zwei Rechtecke im Rechteck – Hinweise für Lehrpersonen»
Flächeninhalte von Vielecken (Geometrie, Flächeninhalte)
Jahrgangsstufe: 7 Schwierigkeitsgrad: 4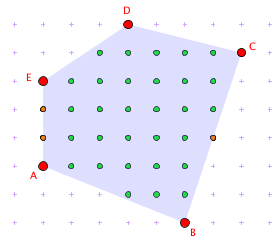
Wie kann der Flächeninhalt von Vielecken in einem Punktegitter berechnet werden?
Link zur mathematischen Situation: «Flächeninhalte von Vielecken»
Arbeitsblatt zur Dokumentation: «Flächeninhalte von Vielecken- Arbeitsblatt»
Hinweise für Lehrpersonen: «Flächeninhalte von Vielecken – Hinweise für Lehrpersonen»
Das Dreieck im Würfel (Geometrie, Würfel)
Jahrgangsstufe: 7 Schwierigkeitsgrad: 2
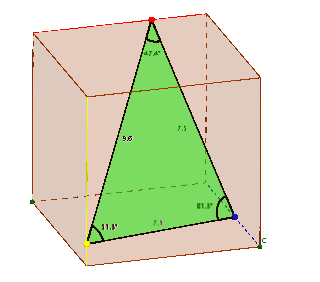
Welche Form kann ein Dreieck im Würfel haben?
Link zur mathematischen Situation in Farbe: «Das Dreieck im Würfel»
Link zur mathematischen Situation mit einer Blau-Rot-3D-Brille: «Das Dreieck im Würfel – 3D»
Arbeitsblatt zur Dokumentation: «Das Dreieck im Würfel – Arbeitsblatt»
Hinweise für Lehrpersonen: «Das Dreieck im Würfel – Hinweise für Lehrpersonen»
Rechtwinklige Dreiecke (Geometrie, Kreis)
Jahrgangsstufe: 8 Schwierigkeitsgrad: 2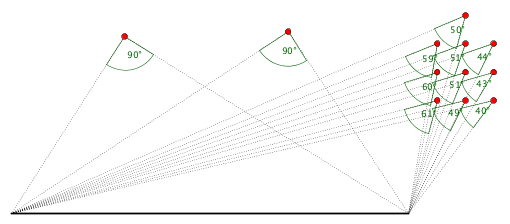
Wo liegen alle Ecken eines rechtwinkligen Dreiecks über einer festen Strecke AB?
Link zur ersten mathematischen Situation: «Rechtwinklige Dreiecke – Entdeckung»
Link zur zweiten mathematischen Situation: «Rechtwinklige Dreiecke – Begründung»
Arbeitsblatt zur Dokumentation: «Rechtwinklige Dreiecke – Arbeitsblatt»
Hinweise für Lehrpersonen: «Rechtwinklige Dreiecke – Hinweise für Lehrpersonen»
Winkel über einer Strecke (Geometrie, Kreis)
Jahrgangsstufe: 8 Schwierigkeitsgrad: 4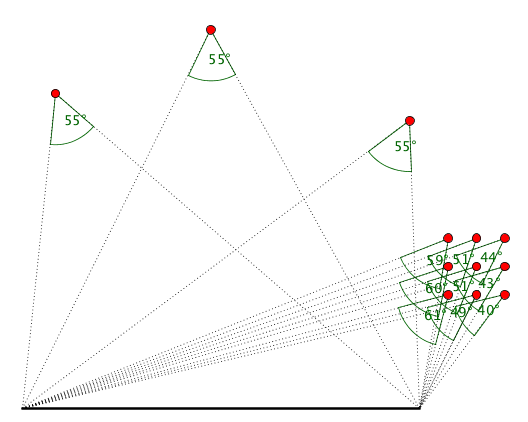
Wo liegen die Ecken von Dreiecken über einer festen Strecke AB mit einem fixen Winkel bei Ecke C?
Link zur ersten mathematischen Situation: «Winkel über einer Strecke – Entdeckung»
Link zur zweiten mathematischen Situation: «Winkel über einer Strecke – Begründung»
Arbeitsblatt zur Dokumentation: «Winkel über einer Strecke – Arbeitsblatt»
Hinweise für Lehrpersonen: «Winkel über einer Strecke – Hinweise für Lehrpersonen»
Der Flächeninhalt des Kreises (Geometrie, Kreis)
Jahrgangsstufe: 8 Schwierigkeitsgrad: 3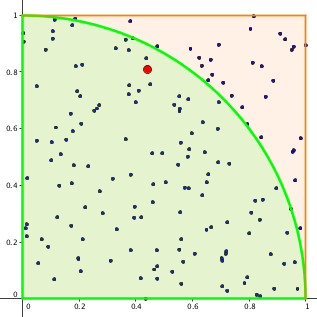
Wie kann mit einem «Punkteregen» der Flächeninhalt eines Kreises berechnet werden?
Link zur mathematischen Situation: «Der Flächeninhalt des Kreises»
Arbeitsblatt zur Dokumentation: «Der Flächeninhalt des Kreises – Arbeitsblatt»
Hinweise für Lehrpersonen: «Der Flächeninhalt des Kreises – Hinweise für Lehrpersonen»
Die rutschende Leiter (Geometrie, Kreis)
Jahrgangsstufe: 8 Schwierigkeitsgrad: 5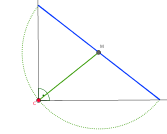
Wie bewegt sich der Mittelpunkt einer Leiter, die entlang einer Wand rutscht?
Link zur ersten mathematischen Situation: «Die rutschende Leiter – Entdeckung»
Link zur zweiten mathematischen Situation: «Die rutschende Leiter – Begründung»
Arbeitsblatt zur Dokumentation: «Die rutschende Leiter – Arbeitsblatt»
Hinweise für Lehrpersonen: «Die rutschende Leiter – Hinweise für Lehrpersonen»
Punkte auf einem rollenden Kreis (Geometrie, Kreis)
Jahrgangsstufe: 8 Schwierigkeitsgrad: 5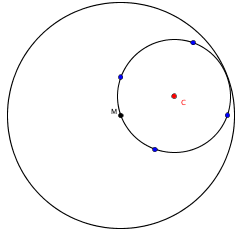
Auf welcher Kurve bewegen sich Punkte eines Kreises, der in einem anderen Kreis abrollt?
Link zur mathematischen Situation: «Punkte auf einem rollenden Kreis»
Arbeitsblatt zur Dokumentation: «Punkte auf einem rollenden Kreis – Arbeitsblatt»
Hinweise für Lehrpersonen: «Punkte auf einem rollenden Kreis – Hinweise für Lehrpersonen»
Der rollende Kreis (Geometrie, Kreis)
Jahrgangsstufe: 8 Schwierigkeitsgrad: 2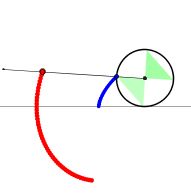
Welche Bahn durchläuft ein Punkt auf einem Kreis, der auf einer Geraden rollt?
Link zur mathematischen Situation: «Der rollende Kreis»
Arbeitsblatt zur Dokumentation: «Der rollende Kreis – Arbeitsblatt»
Hinweise für Lehrpersonen: «Der rollende Kreis – Hinweise für Lehrpersonen»
Link zur mathematischen Situation «in der Nacht»: «Der rollende Kreis (schwarz)»
Der Spirograph (Geometrie, Kreis)
Jahrgangsstufe: 8 Schwierigkeitsgrad: 2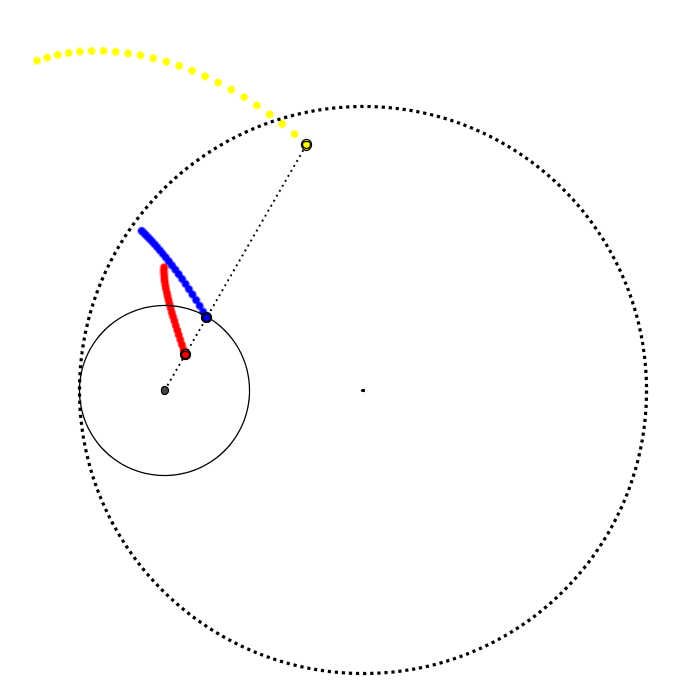
Welche Bahn durchläuft ein Punkt auf einem Kreis, der in einem grösseren Kreis rollt?
Link zur mathematischen Situation: «Der Spirograph»
Arbeitsblatt zur Dokumentation: «Der Spirograph – Arbeitsblatt»
Hinweise für Lehrpersonen: «Der Spirograph – Hinweise für Lehrpersonen»
Link zur mathematischen Situation «in der Nacht»: «Der Spirograph (schwarz)»